Guitar bends
The guitar bend is a technique commonly performed on electric guitars, where the performer pushes strings out of their normal alignment after notes start to sound. Bending strings tightens them, which produces the characteristic pitch fluctuation.
Performing a guitar bend often also involves sustaining the bent pitch before allowing the string to return to its natural position and un-bent pitch. In Dorico Elements, these actions are called a “guitar bend hold” and “release” respectively.

Guitar bends and releases with bend intervals of up to a whole step (tone) are reflected in playback.
- Guitar bends
-
Guitar bends indicate that the performer should bend the string after playing a note, so that the pitch increases while the note sounds. In Dorico Elements, each guitar bend joins two notes: the start pitch and the pitch at the peak of the bend.
On notation staves, guitar bends are notated using an angled line between the noteheads at the start and end. On tablature, guitar bends are notated using an upwards-pointing curved line with an arrowhead at the top and a bend interval above the arrowhead. The fret number of the end note is hidden automatically.
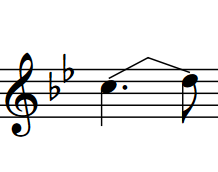
Figure 2. Guitar bend on notation staff 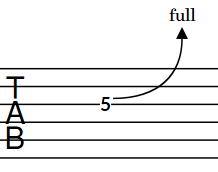
Figure 3. Guitar bend on tablature If you input guitar bends on multiple notes in chords, their arrowheads are automatically aligned on tablature.

Figure 4. Guitar bends on chord on notation staff 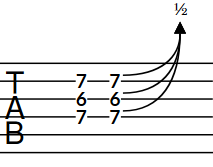
Figure 5. Guitar bends on chord on tablature Sequences of consecutive guitar bends are notated as bend runs on tablature.
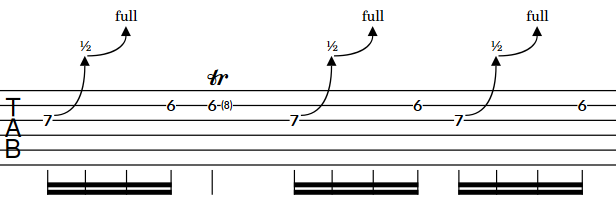
Figure 6. Guitar bend runs on tablature - Guitar bend holds
-
Guitar bend holds indicate that the performer should maintain the pitch at the peak of a guitar bend. They are usually shown on tied notes.
On tablature, guitar bend holds are notated using a horizontal line. They are not notated on notation staves.
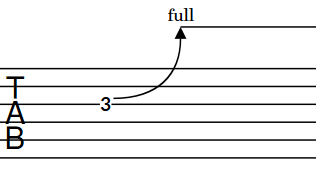
Figure 7. Guitar bend hold on tablature - Releases
-
Releases indicate that the performer should allow a bent string to return to its natural position, which decreases the pitch. In Dorico Elements, each release joins two notes: the pitch at the peak of the bend and the end pitch.
On notation staves, releases are notated using an angled line between the noteheads at the start and end. On tablature, releases are notated using a downwards-pointing curved line with an arrowhead at the bottom and parenthesized fret numbers below the arrowhead to indicate the end pitches. The fret number of the start note is hidden automatically.

Figure 8. Release on notation staff 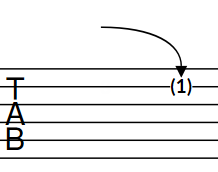
Figure 9. Release on tablature If you input releases on multiple notes in chords, they are notated with a single downwards-pointing curved line on tablature. If the bend intervals are the same for all notes, the end pitches are parenthesized together.

Figure 10. Releases on chord on notation staff 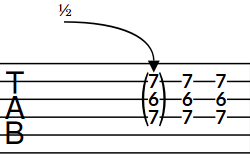
Figure 11. Releases on chord on tablature
-
In addition to guitar bends, Dorico Elements supports guitar pre-bends/pre-dives, guitar post-bends, vibrato bar dives and returns, and other guitar techniques.
-
Because you input releases in the same way as you input guitar bends, in this documentation, “guitar bends” refers to both guitar bend and release items in projects.
-
Stems, stem flags, and beaming always appear stem-up on tablature in single-voice contexts, which means they can collide with guitar bends.